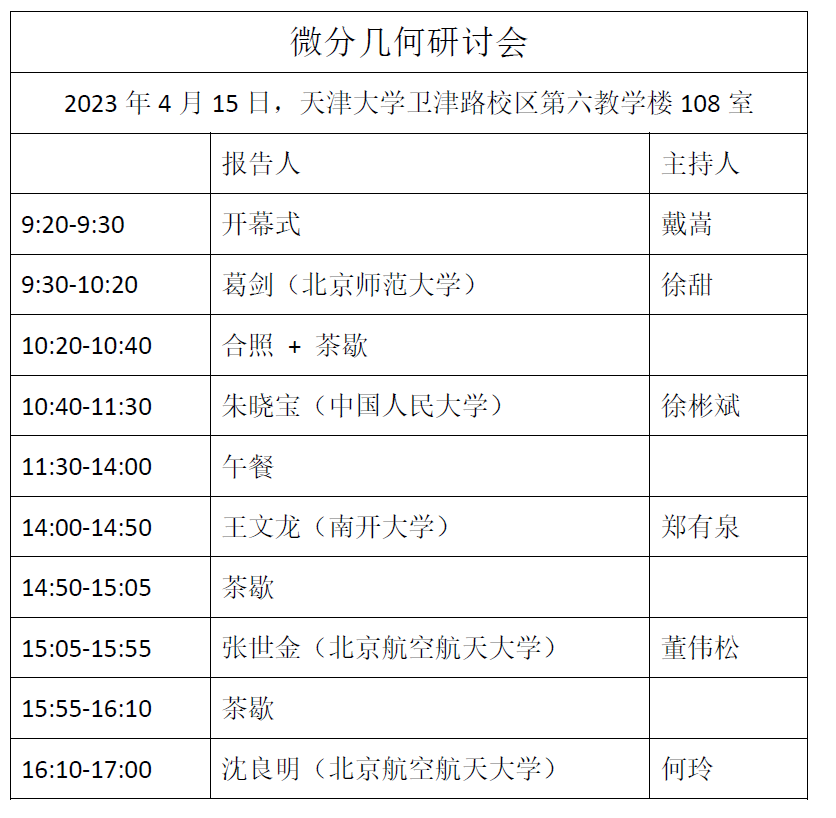
Title and Abstracts:
Jian Ge (Beijing Normal University)
Title: Surfaces with no conjugate points, a survey
Abstract: In this talk, we give a short survey of surfaces without conjugate points. Despite the dimension is two, we know little about the geometry or dynamics of these surfaces. We will focus on open problems and conjectures in this area.
Xiaobao Zhu (Renmin University of China)
Title: Kazdan-Warner equations on compact Riemann surfaces
Abstract: In this talk, we shall review firstly the study history of Kazdan-Warner equations on compact Riemann surfaces, which was proposed by Kazdan and Warner on Annals of Math on 1974. Then we shall show the sufficient condition which was derived by Ding-Jost-Li-Wang (Asian J. Math.,1997). Finally, we shall present our new results on this topic which contains that the prescribed function can change signs.
Wenlong Wang (Nankai University)
Title: Fill-ins with scalar curvature bounded from below
Abstract: Given a triple of Bartnik data and a constant, Gromov asked under what conditions, does/doesn’t the Bartnik data admit a fill-in with scalar curvature bounded from below by the given constant. Philosophically, sufficiently large (in either pointwise or integral sense) mean curvature rules out such fill-ins. I will talk about some known and new results in this direction. This is mainly based on joint work with Wei Guodong at Sun Yat-Sen University (Zhuhai).
Shijin Zhang (Beihang University)
Title: Introduction to shrinking gradient Ricci solitons
Abstract: Shrinking gradient Ricci soliton is as generalization of Einstein metric, is also as a self-similar solution of Ricci flow and as a critical point of Perelman’s entropy. In this talk, I will talk about some properties of the shrinking gradient Ricci solitons and some related problems.
Liangming Shen (Beihang University)
Title: The Kähler-Ricci flow on log canonical pairs
Abstract: We briefly recall Song-Tian's analytical minimal model program. Then we discuss how to establish the existence of the Kähler-Ricci flow on log canonical pairs and finally we give some convergence results when this log canonical pair is of general type.




